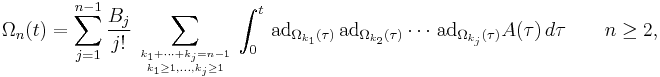Magnus expansion
In mathematics and physics, the Magnus expansion, named after Wilhelm Magnus (1907–1990), provides an exponential representation of the solution of a first order linear homogeneous differential equation for a linear operator. In particular it furnishes the fundamental matrix of a system of linear ordinary differential equations of order 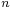 with varying coefficients. The exponent is built up as an infinite series whose terms involve multiple integrals and nested commutators.
with varying coefficients. The exponent is built up as an infinite series whose terms involve multiple integrals and nested commutators.
Contents |
Magnus approach and its interpretation
Given the n × n coefficient matrix A(t) we want to solve the initial value problem associated with the linear ordinary differential equation
for the unknown n-dimensional vector function Y(t).
When n = 1, the solution reads
This is still valid for n > 1 if the matrix A(t) satisfies  for any pair of values of t, t1 and t2. In particular, this is the case if the matrix
for any pair of values of t, t1 and t2. In particular, this is the case if the matrix  is constant. In the general case, however, the expression above is no longer the solution of the problem.
is constant. In the general case, however, the expression above is no longer the solution of the problem.
The approach proposed by Magnus to solve the matrix initial value problem is to express the solution by means of the exponential of a certain n × n matrix function 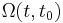 ,
,
which is subsequently constructed as a series expansion,
where, for the sake of simplicity, it is customary to write down 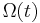 for
for 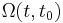 and to take t0 = 0. The equation above constitutes the Magnus expansion or Magnus series for the solution of matrix linear initial value problem.
and to take t0 = 0. The equation above constitutes the Magnus expansion or Magnus series for the solution of matrix linear initial value problem.
The first four terms of this series read
where ![\scriptstyle \left[ A,B\right] \equiv AB-BA](/2012-wikipedia_en_all_nopic_01_2012/I/4716889dd15008b579c23dbdfaa91433.png) is the matrix commutator of A and B.
is the matrix commutator of A and B.
These equations may be interpreted as follows: 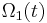 coincides exactly with the exponent in the scalar (n = 1) case, but this equation cannot give the whole solution. If one insists in having an exponential representation the exponent has to be corrected. The rest of the Magnus series provides that correction.
coincides exactly with the exponent in the scalar (n = 1) case, but this equation cannot give the whole solution. If one insists in having an exponential representation the exponent has to be corrected. The rest of the Magnus series provides that correction.
In applications one can rarely sum exactly the Magnus series and has to truncate it to get approximate solutions. The main advantage of the Magnus proposal is that, very often, the truncated series still shares with the exact solution important qualitative properties, at variance with other conventional perturbation theories. For instance, in classical mechanics the symplectic character of the time evolution is preserved at every order of approximation. Similarly the unitary character of the time evolution operator in quantum mechanics is also preserved (in contrast to the Dyson series).
Convergence of the expansion
From a mathematical point of view, the convergence problem is the following: given a certain matrix 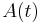 , when can the exponent
, when can the exponent 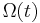 be obtained as the sum of the Magnus series? A sufficient condition for this series to converge for
be obtained as the sum of the Magnus series? A sufficient condition for this series to converge for 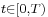 is
is
where 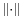 denotes a matrix norm. This result is generic, in the sense that one may consider specific matrices
denotes a matrix norm. This result is generic, in the sense that one may consider specific matrices 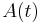 for which the series diverges for any
for which the series diverges for any 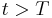 .
.
Magnus generator
It is possible to design a recursive procedure to generate all the terms in the Magnus expansion. Specifically, with the matrices 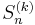 defined recursively through
defined recursively through
one has
Here 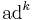 is a shorthand for an iterated commutator,
is a shorthand for an iterated commutator,
and  are the Bernoulli numbers.
are the Bernoulli numbers.
When this recursion is worked out explicitly, it is possible to express 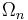 as a linear combination of
as a linear combination of  -fold integrals of
-fold integrals of 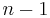 nested commutators containing
nested commutators containing  matrices
matrices  ,
,
an expression that becomes increasingly intricate with  .
.
Applications
Since the 1960s, the Magnus expansion has been successfully applied as a perturbative tool in numerous areas of physics and chemistry, from atomic and molecular physics to nuclear magnetic resonance and quantum electrodynamics. It has been also used since 1998 as a tool to construct practical algorithms for the numerical integration of matrix linear differential equations. As they inherit from the Magnus expansion the preservation of qualitative traits of the problem, the corresponding schemes are prototypical examples of geometric numerical integrators.
See also
- Baker–Campbell–Hausdorff formula
- Fer expansion
References
- W. Magnus (1954). "On the exponential solution of differential equations for a linear operator". Comm. Pure and Appl. Math. VII (4): 649–673. doi:10.1002/cpa.3160070404.
- S. Blanes, F. Casas, J.A. Oteo, J. Ros (1998). "Magnus and Fer expansions for matrix differential equations: The convergence problem". J. Phys. A: Math. Gen. 31 (1): 259–268. doi:10.1088/0305-4470/31/1/023.
- A. Iserles, S.P. Nørsett (1999). "On the solution of linear differential equations in Lie groups". Phil. Trans. R. Soc. Lond. A 357 (1754): 983–1019. doi:10.1098/rsta.1999.0362.
- S. Blanes, F. Casas, J.A. Oteo, J. Ros (2009). "The Magnus expansion and some of its applications". Phys. Rep. 470 (5-6): 151–238. doi:10.1016/j.physrep.2008.11.001.

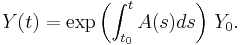
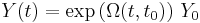
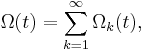
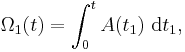
![\Omega_2(t) =\frac{1}{2}\int_0^t \text{d}t_1 \int_0^{t_1} \text{d}t_2\ \left[ A(t_1),A(t_2)\right]](/2012-wikipedia_en_all_nopic_01_2012/I/2cb21f6db4d4213726d4d69235d41479.png)
![\Omega_3(t) =\frac{1}{6} \int_0^t \text{d}t_1 \int_0^{t_{1}}\text{d} t_2 \int_0^{t_{2}} \text{d}t_3 \ (\left[ A(t_1),\left[
A(t_2),A(t_3)\right] \right] %2B\left[ A(t_3),\left[ A(t_2),A(t_{1})\right] \right] )](/2012-wikipedia_en_all_nopic_01_2012/I/16e7c1fd6835c543afb90a29b0fc8503.png)
![\Omega_4(t) =\frac{1}{12} \int_0^t \text{d}t_1 \int_0^{t_{1}}\text{d} t_2 \int_0^{t_{2}} \text{d}t_3 \int_0^{t_{3}} \text{d}t_4 \ (\left[\left[\left[A_1,A_2\right],
A_3\right],A_4\right]%2B
\left[A_1,\left[\left[A_2,A_3\right],A_4\right]\right]%2B
\left[A_1,\left[A_2,\left[A_3,A_4\right]\right]\right]%2B
\left[A_2,\left[A_3,\left[A_4,A_1\right]\right]\right]
)](/2012-wikipedia_en_all_nopic_01_2012/I/8a8f6d75e7ca624e51a53800126dca51.png)
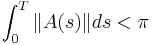
![S_{n}^{(j)} =\sum_{m=1}^{n-j}\left[ \Omega_{m},S_{n-m}^{(j-1)}\right],\qquad\qquad 2\leq j\leq n-1](/2012-wikipedia_en_all_nopic_01_2012/I/6167c94258c39083642d41b24f754d5a.png)
![S_{n}^{(1)} =\left[ \Omega _{n-1},A \right] ,\qquad S_{n}^{(n-1)}= \mathrm{ad} _{\Omega _{1}}^{n-1} (A)](/2012-wikipedia_en_all_nopic_01_2012/I/1af65412f305b1cf466a97e27205ef93.png)
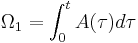
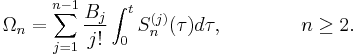
![\mathrm{ad}_{\Omega}^0 A = A, \qquad \mathrm{ad}_{\Omega}^{k%2B1} A = [ \Omega, \mathrm{ad}_{\Omega}^k A ],](/2012-wikipedia_en_all_nopic_01_2012/I/f830a1ca4061c6eefc574a9707f89d0f.png)